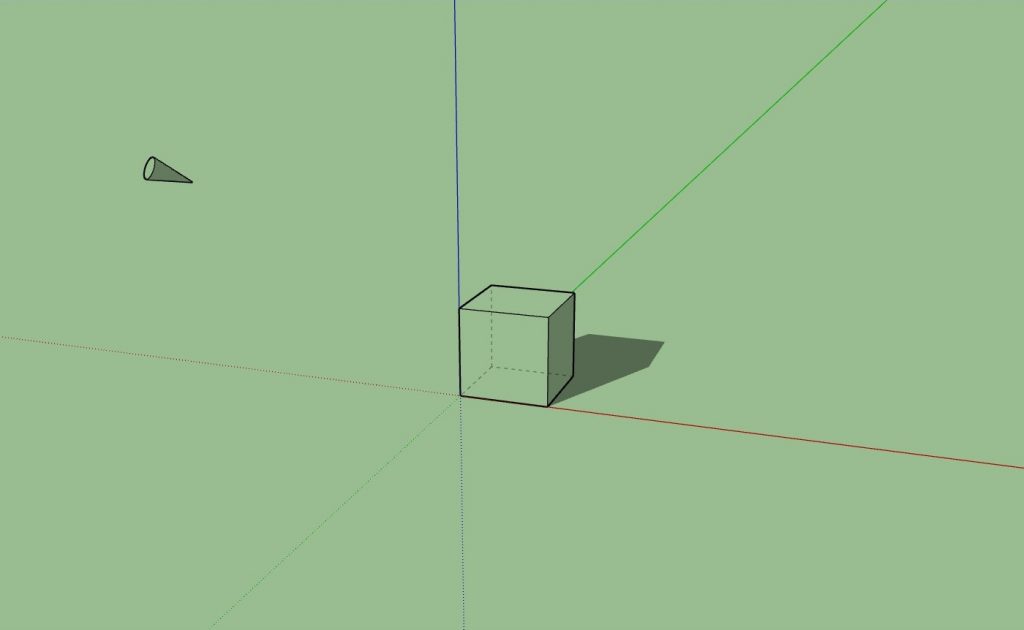图中用圆锥表示出了光源方向，按照经验我们可以很快画出图中立方体的光影。
简单快捷，没有啥难度。如果是一组几何图设计还能这样轻松的画出准确的光影么？

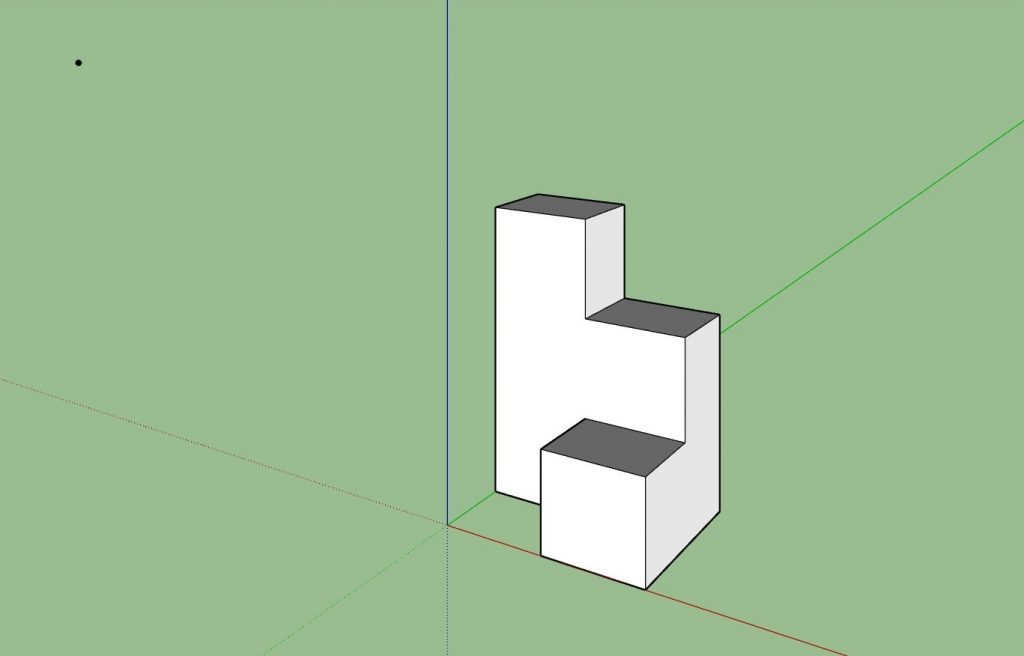这个组合有点复杂，已经没法像一个立方体那样依靠直观经验来画出影子了。要想推算出准确的影子，可以先看看简单的情况，这个情况比立方体还要简单，就是一根立在地上的一根木棍。

我们还可以再简化一下，光源是一个点（没有体积，就是一个数学意义的点），木棍是一个二维的线，将木棍和光源放在一个二维的平面上，看到的影子如下图。

光会延直线传播，所以可以画出影子（用红色标注）。

之所以敢这样简化，是因为对于影子，木棍，光源它们是在同一个平面上的，放到三维空间里也是这样。

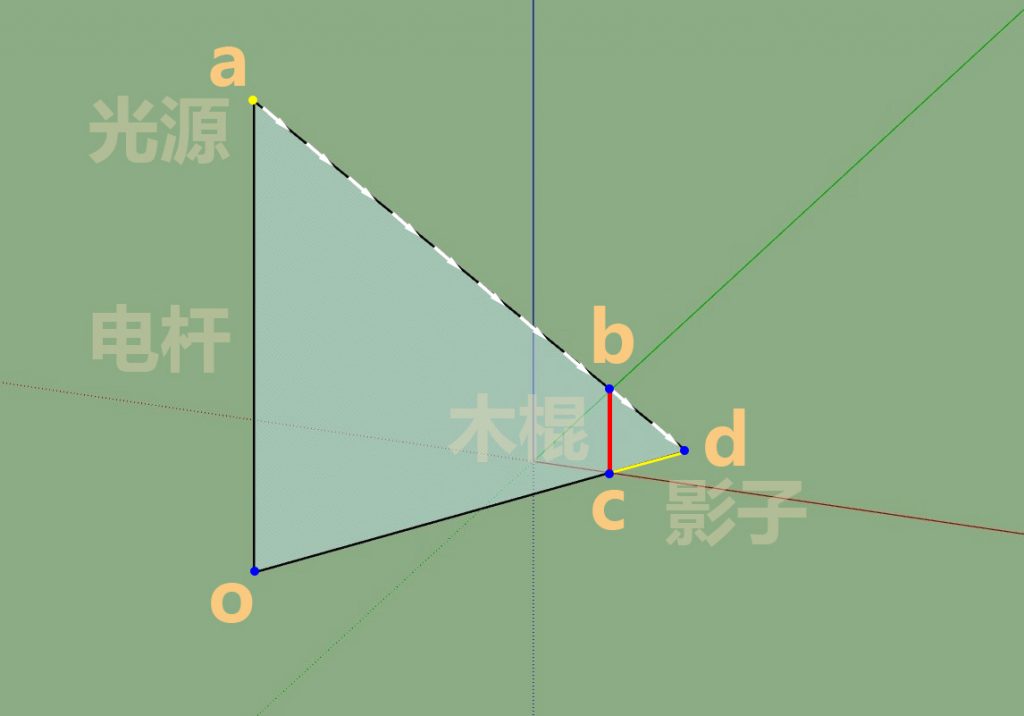注意图上的线。光源与地面的投影是o点，oa相对于是立在地上的一根电杆上有一盏灯照亮了四周。木棍bc垂直于地面，连接oc，ab，这个四边形在同一个平面上。延长oc和ab会得到交点d。d点在地面上，是b点在地面上的影子，也就是影子的末端。连接dc就是木棍在这个光源下的影子。

一根木棍的情况了解了，再看看同一个地面上有很多木棍的情况，如下图。

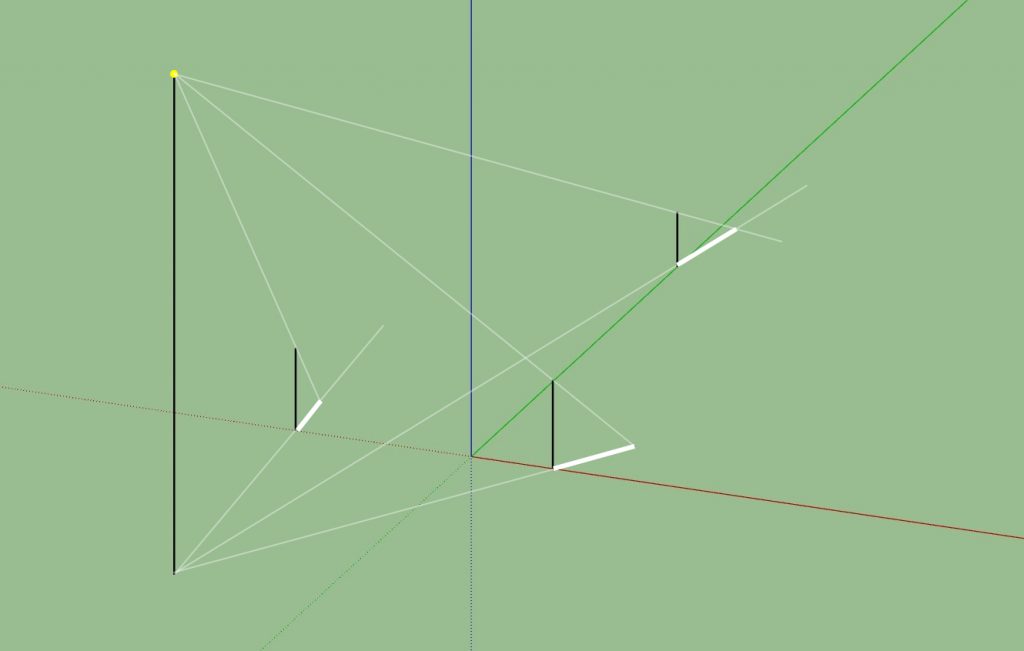
就是重复画出一根木棍的影子方法，对每一根木棍再画了一次。

这下可以说立方体的影子了。

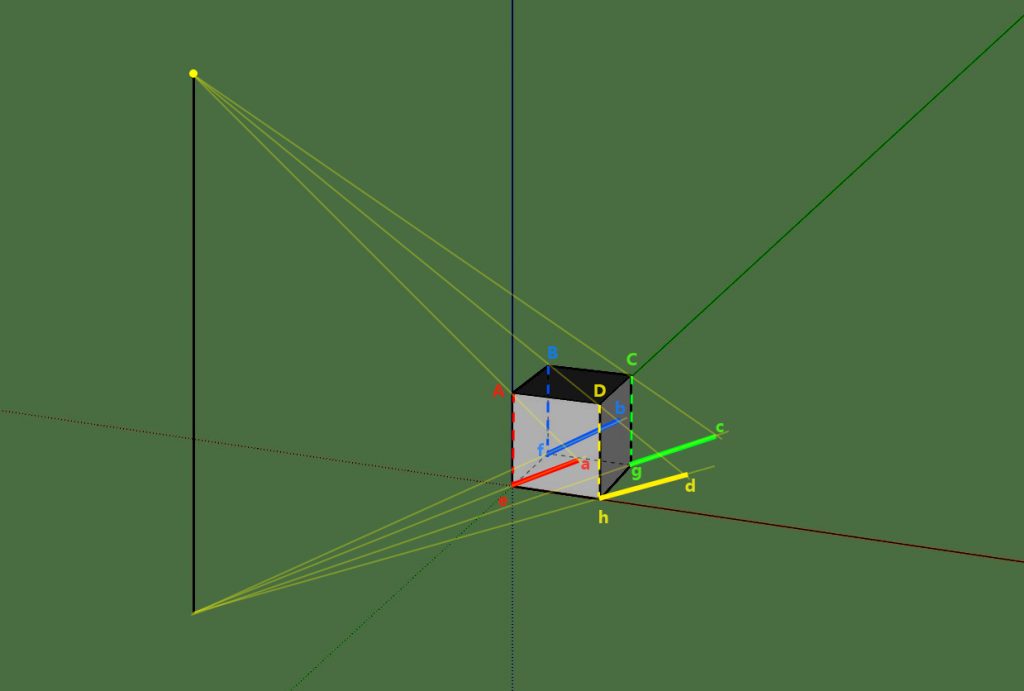分别找出图中红黄蓝绿四条棱的影子（虚线）。立方体上的ABCD四点在地上的投影分别是abcd，按顺序连接四点（abcd）就可以得到立方体顶面（由ABCD构成）在地面上的影子。

ae就是AE棱的影子，abfe是ABFE的影子，其余的面同理，就不一一列出了。

如果立方体是个不透明的物体，它在地面上的影子就是abcdefg。

总结一下，这里用到的方法就是先找到点的影子，再将点连成线，由线连成面。找点的投影，是将光源和影子放在一个特殊的平面里，这个平面垂直于地面。

现在我们可以挑战一个复杂的组合体了。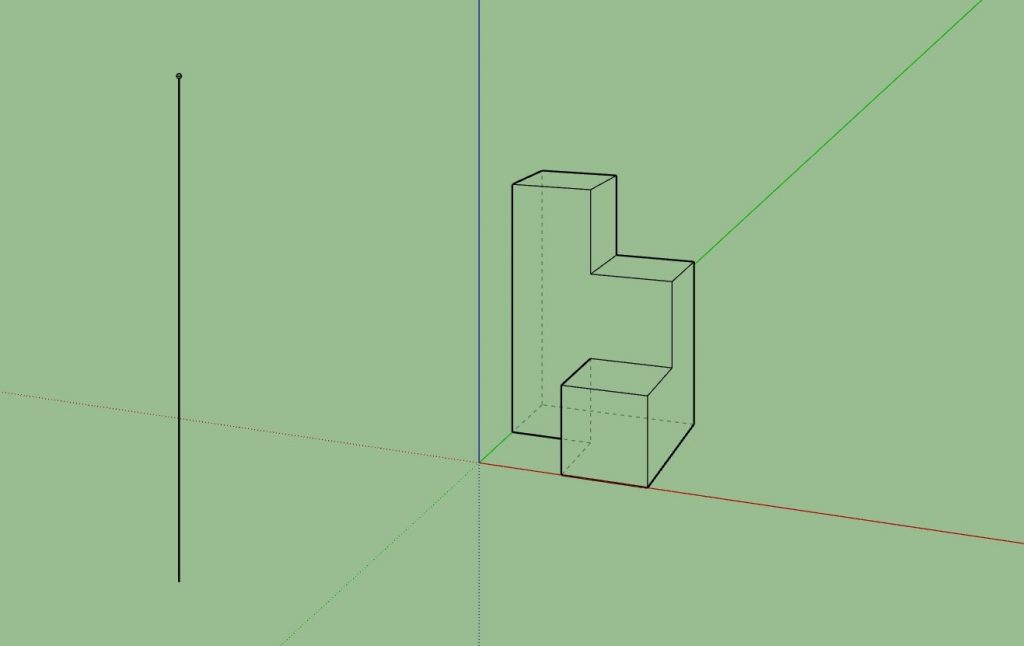

首先将组合体上的红点在地面上的影子位置找出来（黄点）。

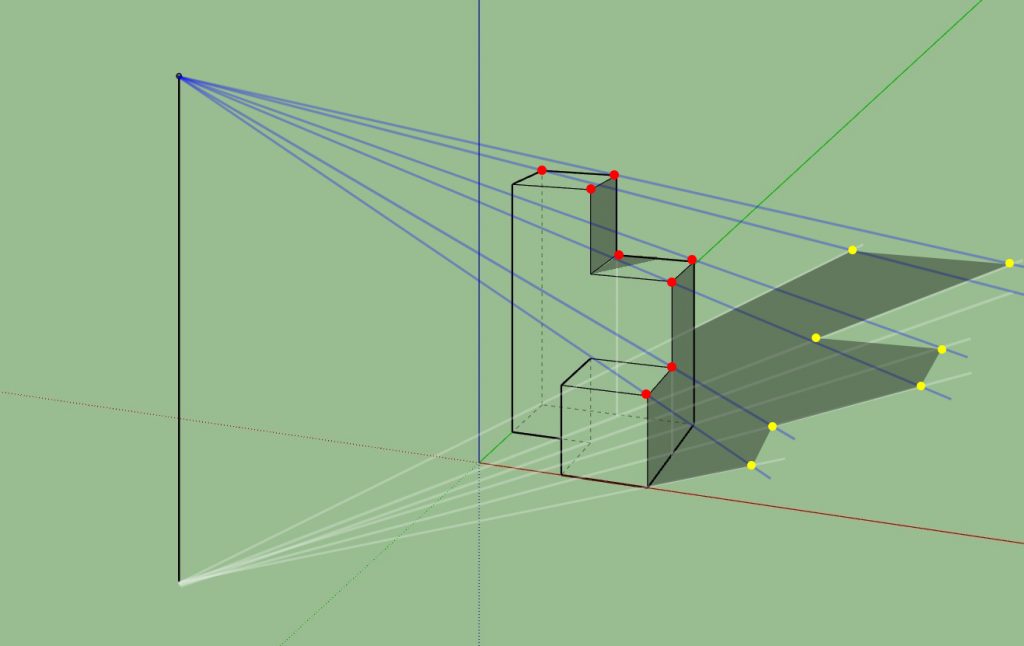
然后将红点的投影与物体底部的对应点连接起来，就可以围出阴影面。

对于这种复杂组合，可以理解为由很多个立方体组成的物体，用找点，连线，出面的方法可以得到一个准确的影子。

这里只是一个开始，绘画会遇到的情况会更加复杂，曲线的，遮挡的情况留在下一篇再说。